Time limit 2000/4000/4000/4000 ms. Memory limit 65000/65000/65000/65000 Kb.
Prepared by Ibrahim Mesecan.
Center of gravity of a plate
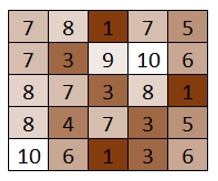National Science academy, for an experiment, needs to
calculate the center of gravity (weight center)
of an irregular plate. The plate has tabular format and
it has different weights on its every cell
(e.g. the left figure).
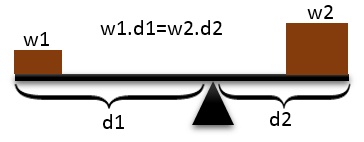In physics, center of gravity is the
point where relative distributed mass sums to zero.
Center of gravity of a rectangular-irregular shape is the
point where the difference between sum of weighted
relative positions on the left-right and up-down
sides are close to zero.
Assuming that
- the objects have fixed width (1cm each)
- all objects are pin-point objects and have their
center of gravity in their centers (5mm, 5mm)
For example, if we have the following 5-by-1 rectangular
object (right image) with the weights: 2, 3, 1, 1, 3.
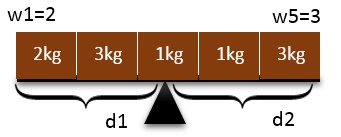Then, the weight center of the series is 2.5cms
from the left and 0.5cms from the top. Because
2*2 + 3*1 + 1*0 = 1*1 + 3*2
and thus sum of weighted relative positions on the left
and right sides are equal to zero.
Question: Write a program that
is going to read the weights on a rectangular object
and decide the center of gravity.
Input specification
There are two numbers (m and n) at the beginning representing
height and width of the rectangular object. Each of the
following m lines have n-integers numbers where
1 ≤ (m and n) ≤ 1000, and the numbers are between 0 and 100.
Output specification
Show x and y positions of weight center with
a 0.01cm precision.
| Sample Input I |
Sample Input II |
3 3
1 2 2
1 2 2
4 8 8
|
4 4
15 22 16 19
14 7 15 10
7 12 4 17
19 2 14 7
|
| Sample Output I |
Sample Output II |
1.7 2 |
2 1.76 |
Explanation: You can use the following
formula to calculate the centers:
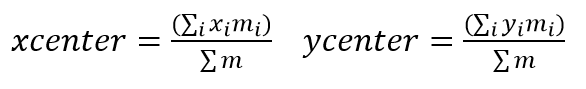
Для отправки решений необходимо выполнить вход.
|