Time limit 2000/4000/4000/4000 ms. Memory limit 65000/65000/65000/65000 Kb.
Prepared by Ibrahim Mesecan.

Gaussian Elimination
Gaussian elimination, also known as row reduction,
is a method to solve linear equations. The method is
named after famous mathematician Carl Friedrich Gauss.
The equation ax1 + bx2 =
c is called as linear equation
where a, b and c are numerical coefficients and xi
is called as unknown variable. The previous equation has
two unknowns. And, the following equation has three unknowns
ax1 + bx2 + cx3 = d.
In order to solve a linear equation with n unknowns,
you need to have n (distinct) linear equations.
Note: The solution steps are explained in
this document.
Question: You will be given n-linear
equations with n-unknowns. Calculate the unknown
variable values and show them.
Input specification
You will be given an integer in the beginning:
the number of unknowns (n). In the following n lines,
you will be given n integers
where 0 ≤ n ≤ 50. The following n lines will give
the result of n linear equations.
Output specification:
Show n floating point numbers with 3 digits precision
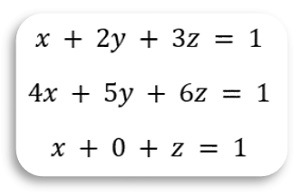
Sample Input
3
1 2 3
4 5 6
1 0 1
1
1
1
|
Sample Output
0 -1 1
|
Explanation:
There are three linear equations given where
the first equation is x + 2y +3z = 1.
The coefficients are 0, -1 and 1. Then,
the first equation means:
(1 * 0) + (2 * -1) + (3 * 1) = 1
Для отправки решений необходимо выполнить вход.
|