Feedback | | If you notice incorrect translations in Contester, please let author know.
|
|
Time limit 2000/4000/4000/4000 ms. Memory limit 65000/65000/65000/65000 Kb.
Question by Ibrahim Mesecan.
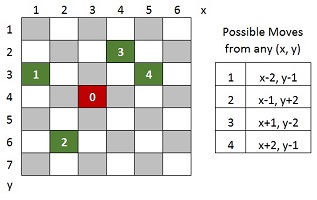
Dynamic Knights
Your knights had limitations therefore they could
fight in a smaller area. Now, they have taken
algorithms course and they are dynamic knights
who can fight in a wider area: 400 x
400 board. See the image for orientation
and possible moves. If you are given the
initial (xi, yi)
and the final (xf, yf)
coordinates, and if you are also given m
positions which are occupied by other pieces
where the knight cannot move on them.
Question:
Write a program that tries all possible moves
and decides the fastest move where the knight can
move over the destination (xf,
yf) cell.
Input specification
Firstly, you will be first given 2 integers
- The size of the board (n) where the board is
an nxn matrice and 1 ≤ n ≤ 400
- The number of cells (m) occupied by other pieces
where 0 ≤ m ≤ 5000
Then in the following line you will be given four
integers initial (xi, yi position
of the knight and the position that the knight wants
to reach (xf, yf). Then, in the
following m lines you will be given (x,y) coordinates
of m occupied cells.
Output specification
Show the minimum number of moves that the knight can
reach to the destination. Show -1, if the knight
cannot reach to the destionation.
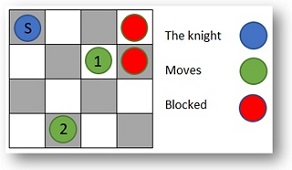
Sample Input I
3 1
1 1 2 2
1 2
|
Sample Input II
4 2
1 1 2 4
4 1
4 2
|
Sample Output I
-1
|
Sample Output II
2
|
Для отправки решений необходимо выполнить вход.
|